Statistical Models for Interaction Data

Models for interaction data are of increasing interest in the machine-learning, complex systems, and statistical literature. Examples of interaction data include email data, where a simplified interaction would be a sender $s$ and a set of receivers \(r_1, r_2, \ldots r_k\), or social media data, where an interaction could be a single posting consisting of a poster \(p\) and commenters \(c_1, c_2, \ldots, c_l\). In full generality, the interaction could include other components, such as the time \(t\) of the interaction, or relevant interaction features like the content of the email.

For models to be useful, it is vital that they reflect observed properties of real-world networks, such as sparsity, clustering, and power-law or scale-free behavior. Many models, such as the stochastic block model and related variants which seek to find clusters within the data, are node-exchangeable, meaning that the permutation of the labels of the nodes does not change the likelihood of the observed network. As a result of this property, it can be shown that data generated from these models cannot be sparse or capture scale-free behavior, both of which are often seen in real-world networks.

Recently, an alternative approach has emerged for modeling network data by treating the edge, or interaction, as the statistical sampling unit. This is particularly natural in the context of many datasets, such as email networks, social networks, and co-authorship networks. For such data, it is valuable to impose exchangeability on the edges as opposed to the nodes. These edge exchangeable models have generated recent attention and are able to exhibit both sparsity and power-law behavior.

Hierarchical Interaction Exchangeable Models

Previous edge exchangeable models cannot account for complex hierarchical structure in interactions. For instance, an email has a hierarchical structure induced by a sender and its many receivers, and a movie can be thought of as an interaction with multiple sets of individuals, such as directors, actors, and screenwriters. As an example, we show local degree distributions of an email dataset, for six of the most populous senders. We note that each sender has unique behavior and further that each sender will have different receivers that are popular with that sender.

In order to account for this heterogeneity, we have created a new model termed the Pitman Yor vertex components model (PY-HVCM). We show through a variety of posterior predictive checks and prediction measures that we outperform similar interaction exchangeable models that do not take into account this hierarchical structure, as well as other state-of-the-art network models. We also apply the model to an arXiv dataset, and using the model are able to show strong clusterings of the subjects on arXiv.

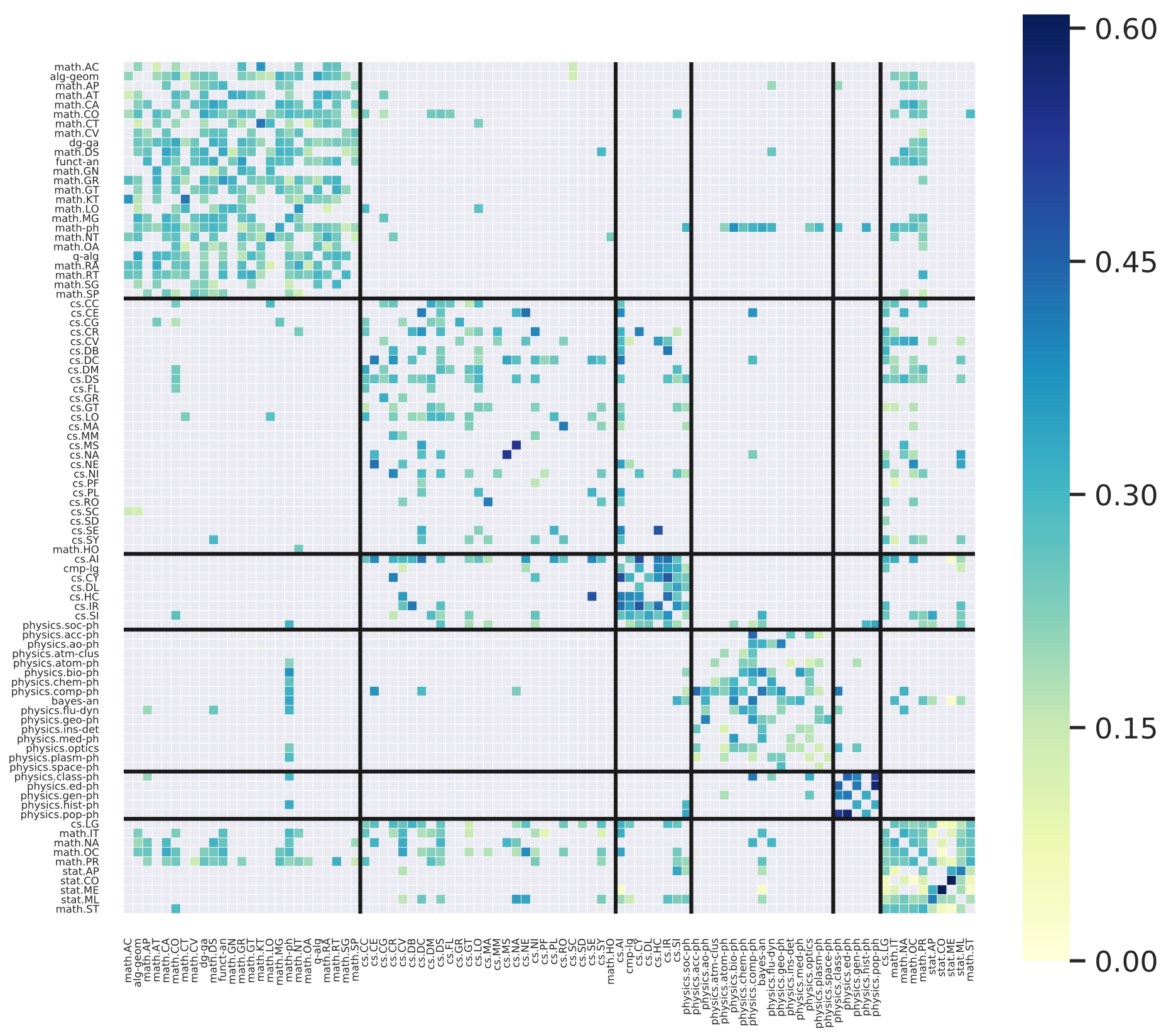
Temporal Interaction Exchangeable Models

Coming soon!

Relevant pubications: