Graph Based Estimation of Information Theoretic Quantities

The estimation of information theoretic quantities is a problem of interest arising not only in information theory, but also feature selection, structure estimation for graphical models, and training and understanding deep neural networks. Common examples of these quantities include Shannon mutual information and KL divergence. In general, these quantities can be difficult to compute for continuous random variables, and most methods rely on an intermediate density estimator for the underlying distribution. These “plug-in” estimators suffer from bias near the support boundaries of the marginal densities and can be computationally prohibitive. Graph based estimation methods aim to skip the density estimation stage and directly estimate the quantity of interest by calculating a graph structure over the data sample. We give two examples from our past work below.

Estimating Multi-Class Bayes Error Using a Graph Based Estimator

Past work has used a minimal spanning tree or k-NN graph to estimate information-theoretic quantities of interest. One of the original algorithms in this area was for the estimation of Henze-Penrose (HP) divergence, which is a member of the broad class of \(f\)-divergences. This divergence measure has two important properties. First, it is possible to estimate the HP divergence directly from a minimal spanning tree across the data sample. As the minimal spanning tree can be computed in $O(n\log n)$, this approach to estimation is amenable to large datasets. Second, tight bounds have been proved that relate the HP divergence to the Bayes error rate of a binary classification problem. Thus, accurate estimation of the HP divergence allows for learning of the intrinsic hardness of the supervised learning task. Although tight bounds exist for the Bayes error rate for a binary classification task, this is not true for multi-class classification. In our work we derive tight bounds for the multi-class case using a generalized Henze-Penrose measure, and provide a graph based estimation procedure using a minimal spanning tree.

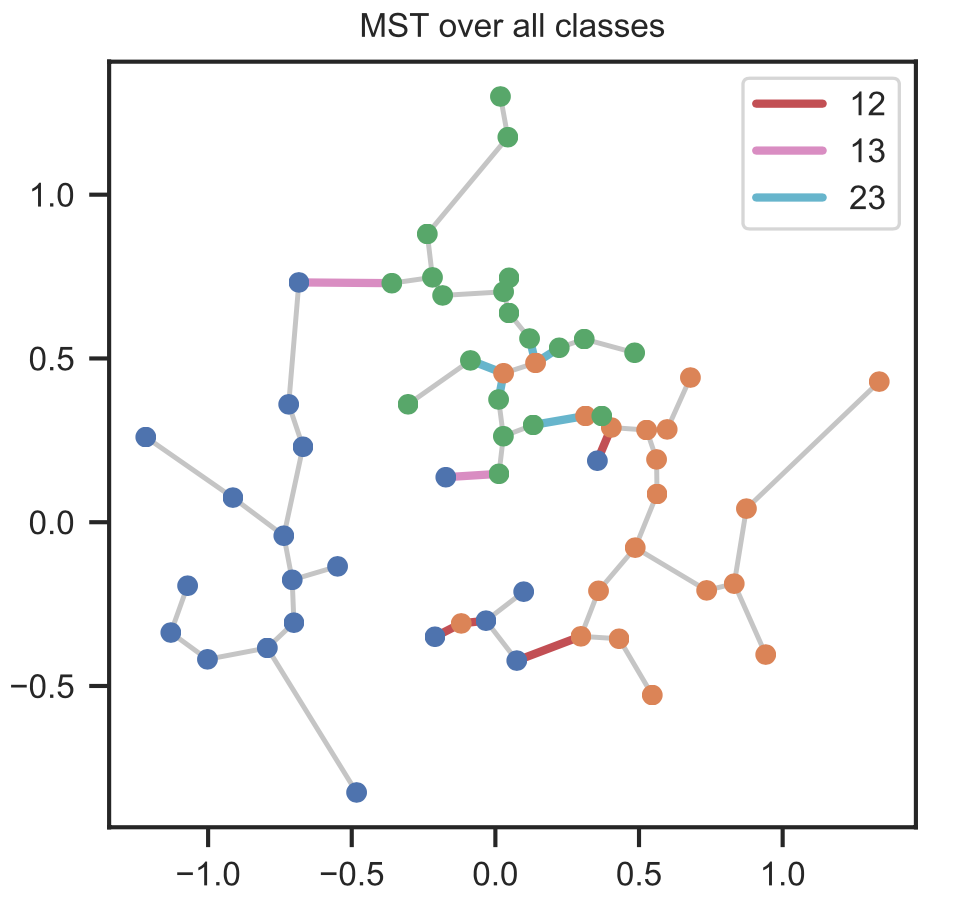
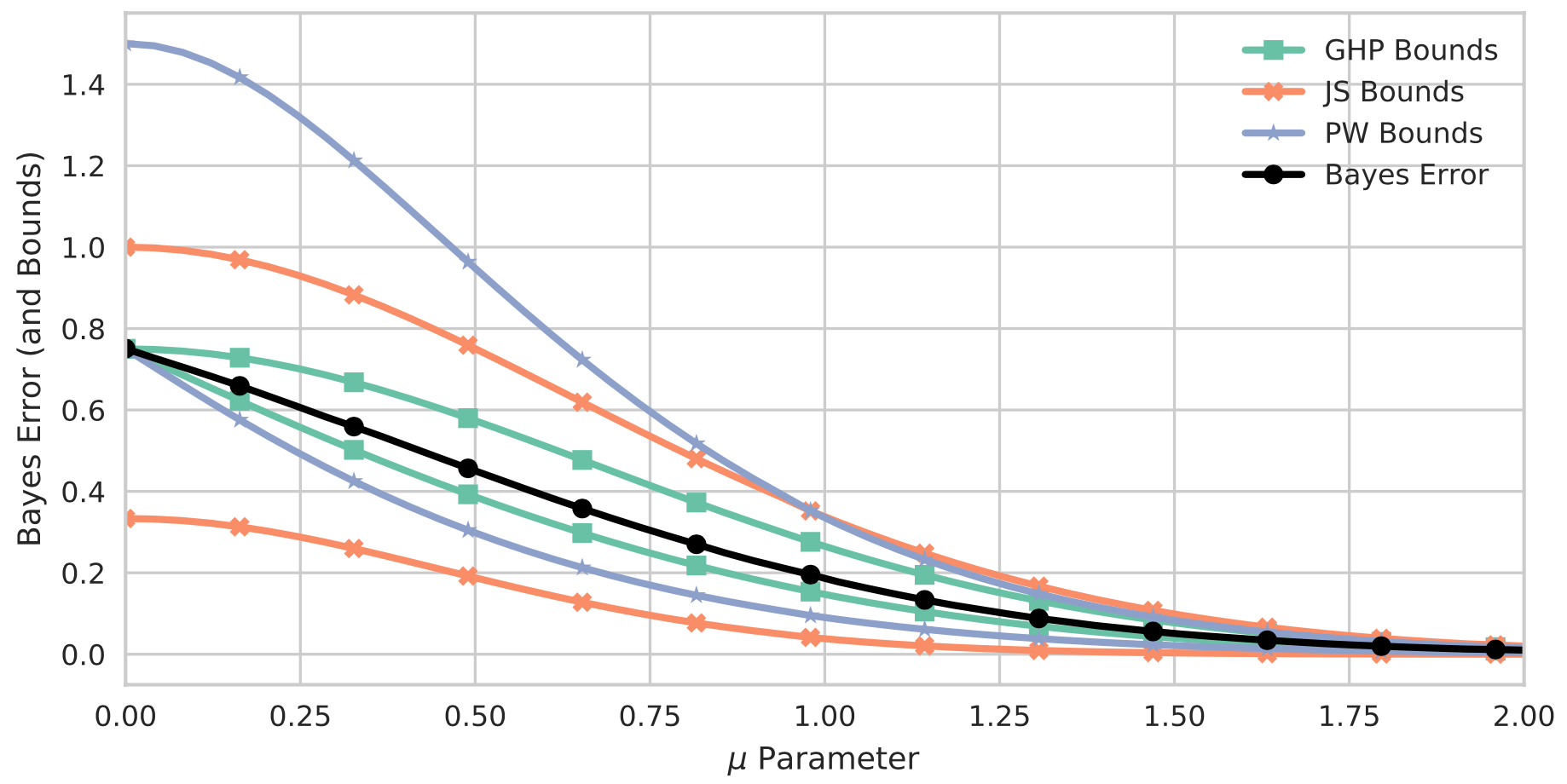
Curbing the Curse of Dimensionality with a New Estimator

Like other estimation methods, graph based estimation methods are subject to the curse of dimensionality. Specifically, as the feature dimension of the data increases, the bias of the estimate also increases. In recent work, we introduce a new estimator of the HP divergence, based on a different computed graph, that reduces the bias for growing dimension.

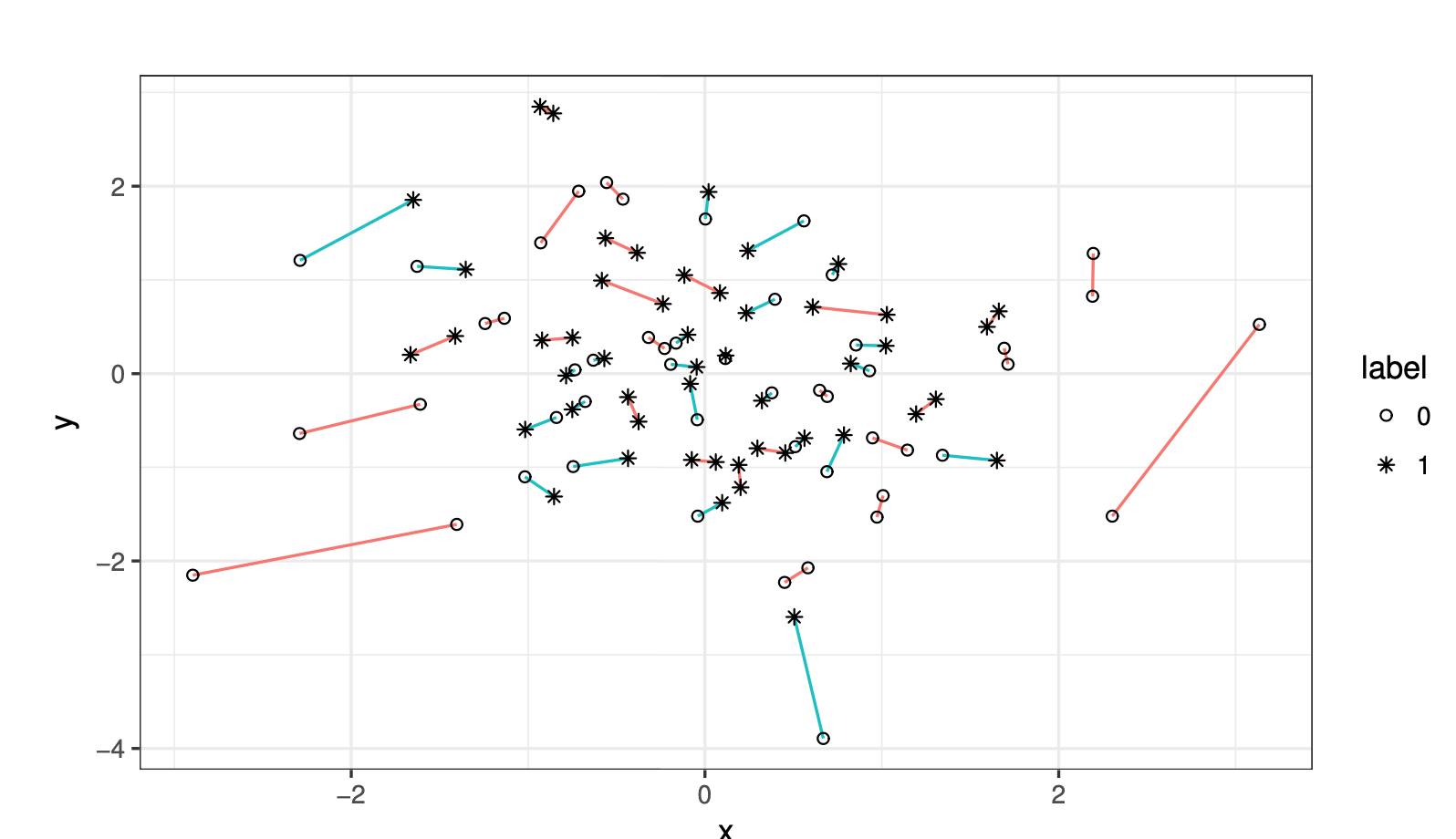
Relevant pubications: